今天我們來看看Binary Search類型的題目吧！還記得當初我們提到Binary Search的時候，會覺得這個演算法也不是特別的難，確實如果說單純搜尋一個特定的值的這種案例來說，不會特別的難，但是其實Binary Search有許多超乎你我想像的功能，以下是我重點的整理。

1. Binary Search可以一次忽略掉一半的資料。
2. 如果我們要找的答案在一個數字區間中，這區間內的數字是有順序性的，而且我們又必須一個一個找才知道，這時就可以嘗試使用Binary Search。

範例1-First Bad Version

我們先來看這一題，題目說我的版本到某一版後就壞掉了，但在那一版之前都是正確的，要求出壞掉的那一版。

1. Brute Force: 暴力破解的解法其實很直觀，就是從第一版開始檢查，當我檢查到錯的那版，我就Return。這樣的時間複雜度是O(n)。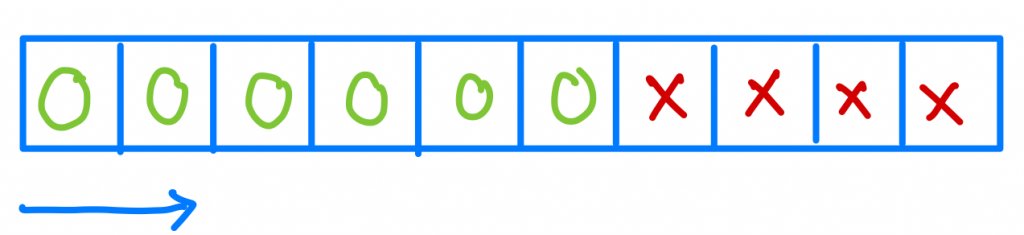
   

2. 我們來把圖畫出來看看，這個問題視覺化後會長的怎麼樣。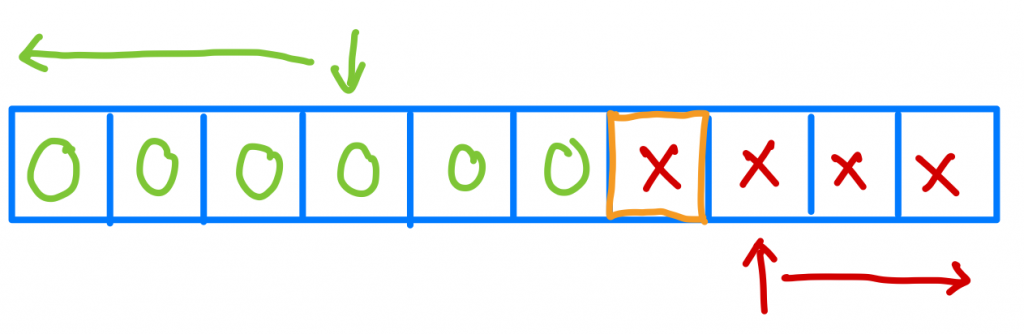
   
   我們要找的是甚麼呢？是要找第一個叉叉出現的位置。我們會發現圈圈的左邊一定都是圈圈，同樣的叉叉的右邊也都一定是叉叉，假如我的版本總共有100，我現在看第70版發現他是叉叉，那就代表70~100都會是叉叉，也就代表答案會在1~69內了。
   反過來說，如果我今天第50版是圈圈那就帶表1~50都是圈圈，換句話說，答案就在51~100裡面了。

這邊我們用 Binary Search 就可以有一個概念，如果mid是圈圈，那就代表我們可以忽略左邊的部分往右邊搜尋，
相反的，如果是叉叉，那就代表我們可以忽略右邊的部分往左邊搜尋，這樣我們就可以再O(logn)時間內完成囉。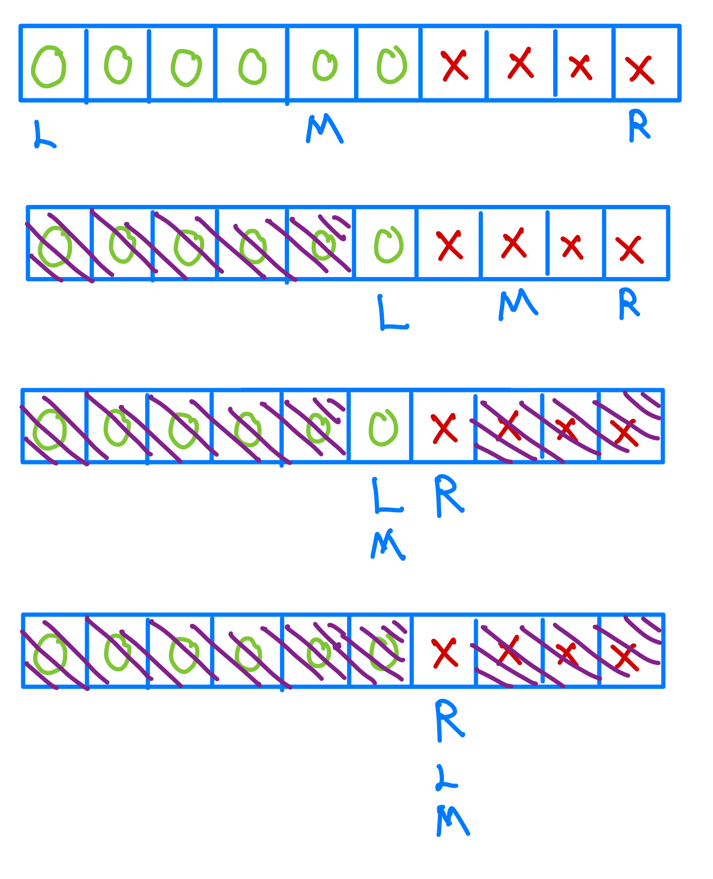

class Solution:
    def firstBadVersion(self, n: int) -> int:
        left = 1
        right = n
        
        while right >= left:
            mid = (left+right) // 2
            if not isBadVersion(mid):
                left = mid + 1
            else:
                right = mid -1

        return left

範例2-Koko Eating Bananas

接著我們來看這一題，這題蠻有趣的，它的題目有一點長也有一點難懂我在這邊稍微解釋一下。
我們可以看到我們有len(piles)那麼多群香蕉，每群香蕉有piles[i]個，我要在h小時內全部吃完，我「最少」一個小時要吃幾根？
說真的如果是第一次看到這種問題，我還真的不知道怎麼處理，所以如果有讀者是第一次看到也無從下手的話，就不用挫折拉哈哈。
首先我們可以來想看看，我「最多」一次吃幾根我可以確保在h小時內吃得完？答案很簡單吧，就是piles裡面最大的值囉！那如果不管吃不吃的完的情況下，最小我可以一次吃幾根，答案是一根對吧，當然我一個小時吃1根是有很可能吃不完的，但沒關係大家繼續往下看。
所以我可以知道max值一定是吃得完，1可能會吃不完，那是不是在1到max值中間存在一個值它可以剛好吃完的呢？所以我把剛剛討論完的想法畫圖給大家看。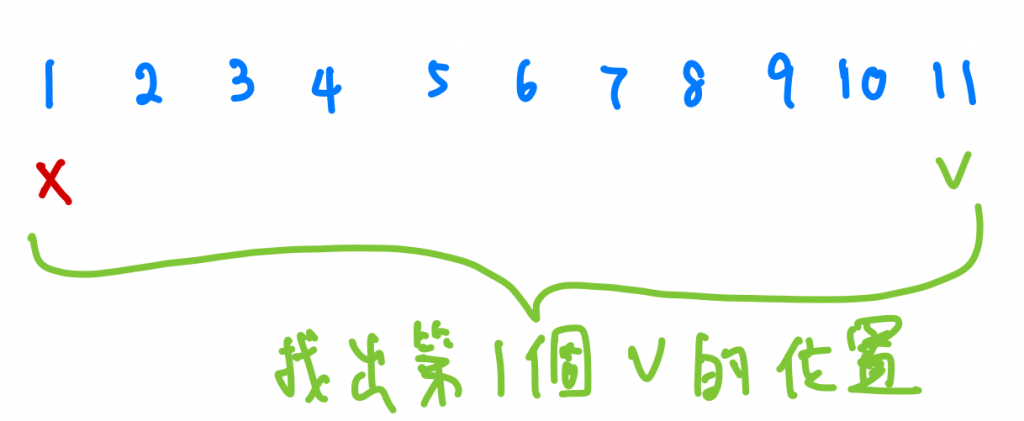

有沒有發現這題根本就是上一題我們做的First Bad Version概念，只差在我們要去寫出「一個小時內吃n根，我在h小時內有沒有辦法吃完piles的一個副函式」，這個副函式其實也真的不難大家可以想看看要怎麼寫，那其他的邏輯就跟上一題一樣囉！

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        
        min_val = 1
        max_val = max(piles)
        
        def can_finish(piles, k, h):
            time = 0
            for pile in piles:
                if k > pile:
                    time += 1
                else:
                    time+=math.ceil(pile/k)
            return False if time > h else True
        
        r = max_val
        l = min_val
        
        while r>=l:
            
            mid = (r+l)//2
            
            if can_finish(piles, mid, h):
                r = mid - 1
            else:
                l = mid + 1
            
        return l

範例3-Search in Rotated Sorted Array

這一題其實我個人覺得比較算是一個特立獨行的問題，在日常中應該比較不會遇到，但是可以理解他的話會發現它也是相當有趣的。
這題一看題目就知道，一定是要用Binary Search來解的，我們就來分析看看吧！
首先一般的Binary Search，因為整個Array都是排序好的情況，所以我們可以很輕易的知道要捨去哪一半。
這一題雖然Array也是排序過後的，但是排序過後我們又將它移花接木一下，變得好像不太容易用Binary Search來處理，我們一步一步來看吧。

我們的Array變成左右半邊兩個部分，這兩個部分的交接處就是最大的值到最小的值那邊。

我們接著來看左右半邊分別有甚麼特點吧！

左半邊的部分

現在假設我們mid index所指向的值為8，大家可以注意到的是，8是在我們左半邊的部分，這個部分的數值有幾個特點，首先我左邊的值一定比我還要小，但是我右邊的值可能比我小，也可能比我大。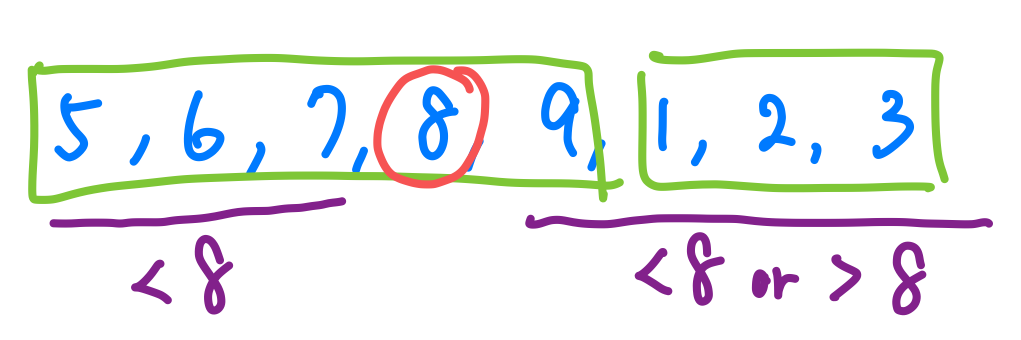

換句話說，如果我要找的數字比8還要大，那我要往右搜尋就可以。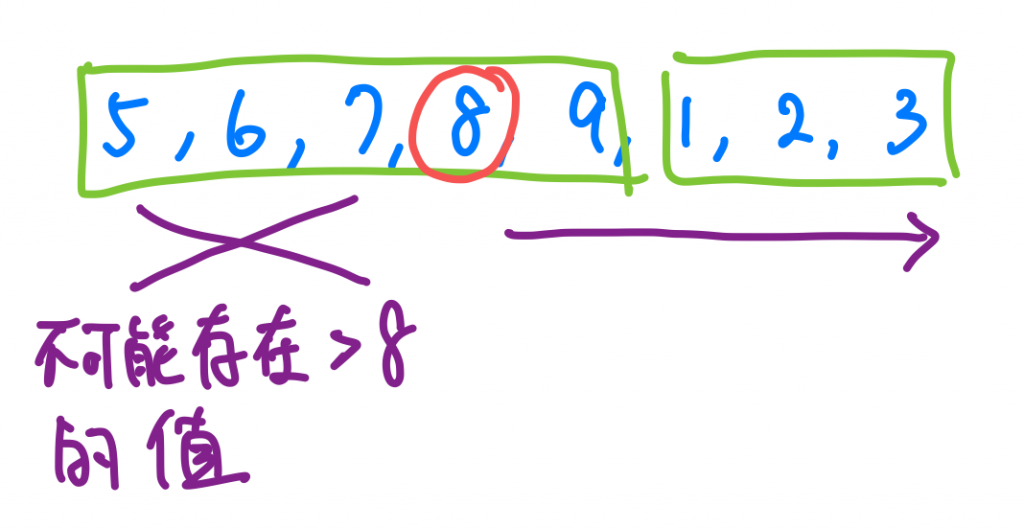

如果比8還要小，兩邊都有可能，但是實際上會是哪邊呢？大家可以發現，我左半邊那群的最小的數字，是會大於右半邊那邊最大的數字的。所以假如我要找的target是1，我發現1比我最左半邊最小的數字5還要小，那我就可以確定我要往右找啦！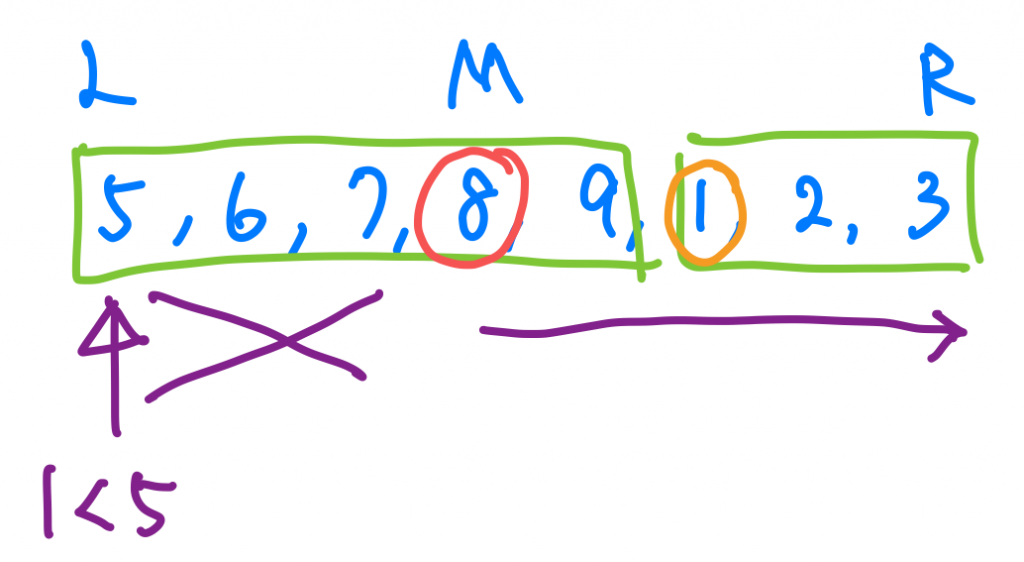

那如果我要找6，我們會發現6比8小但是比5大，那我們就要往左找囉！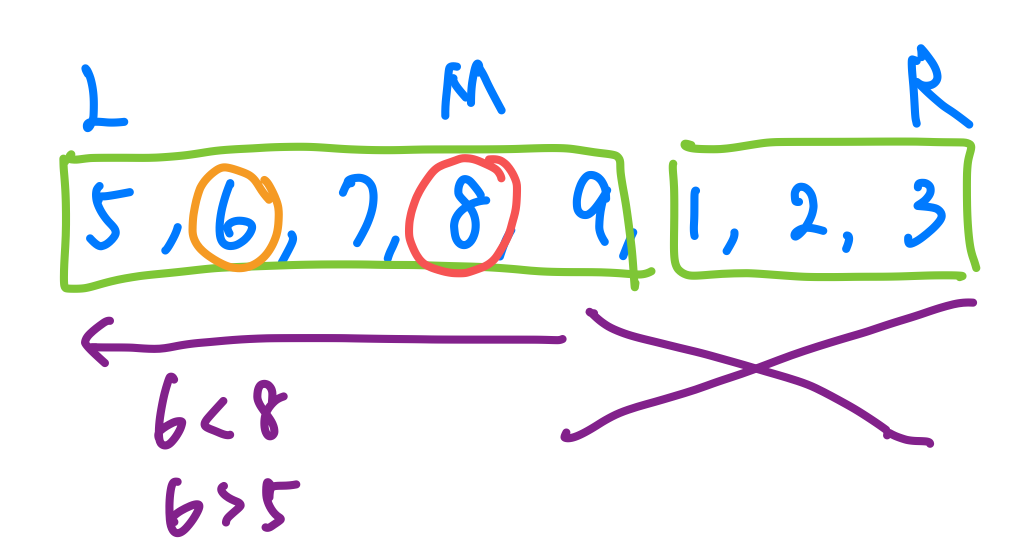

右半邊的部分

那右半邊的部分呢？其實就是跟左半邊的部分倒過來而已啦！假設我現在在2我要找的數字小於2，那我一定只會往左搜尋，相反的，如果大於2那左右都有可能，但是我們一樣可以發現，我右半邊的部分的最大值是會小於左半邊的最小值的，所以一樣利用這個特性，我們可以知道我們要搜尋的是左半邊還是右半邊，其餘的我就不贅述囉！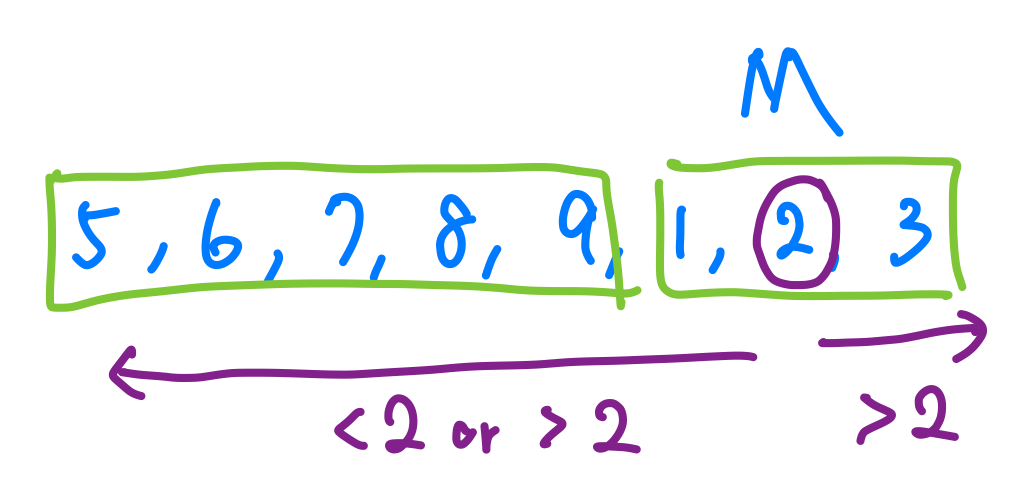

依照上面講完的邏輯我們可以列幾個條件出來

• 如果我在左半邊
  • target > mid value: 往右找
  • target < mid value and target < left value: 往右找
  • target < mid value and target > left value: 往左找
• 如果我在右半邊
  • target < mid value: 往左找
  • target > mid value and target < right value: 往右找
  • target > mid value and target > right value: 往左找

最後如何知道我在左還是右半邊呢？其實很簡單，用自己跟left做比較，如果大於等於就是在左半邊，不然就是右半邊囉！

這時候讀者可能會有疑問，這樣的邏輯適用在沒有Rotated的Sorted Array上嗎？其實是可的，我們可以發現，如果是這種情況，我們會把它當作左半邊部分的Array在跑，在套用上面的邏輯就會發現，這都是行得通的啦！

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        
        left , right = 0, len(nums)-1
        
        while left <= right:
            
            mid = (left + right)//2
            
            if nums[mid] == target:
                return mid
            
            # left part
            if nums[left] <= nums[mid]:
                if target > nums[mid]:
                    left = mid + 1
                else:
                    if nums[left] > target:
                        left = mid + 1
                    else:
                        right = mid - 1
            
            # right part
            else:
                if target < nums[mid]:
                    right = mid - 1
                else:
                    if nums[right] < target:
                        right = mid - 1
                    else:
                        left = mid + 1
        return -1